Category: data structures

Categories
data structures java two pointer

two pointer algorithm

two pointer algorithm

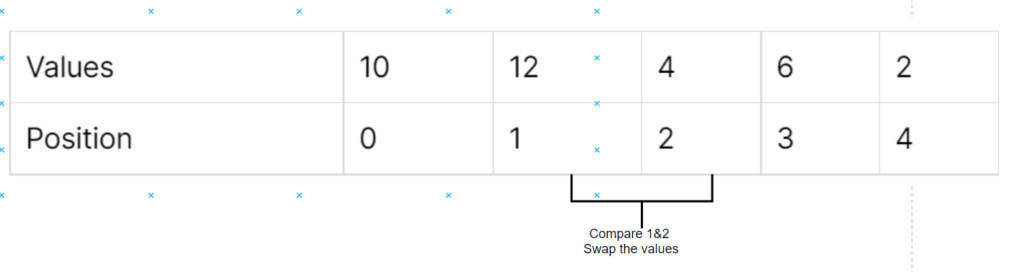
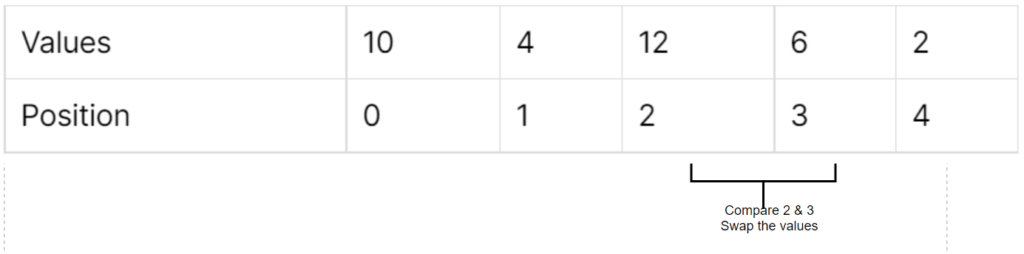
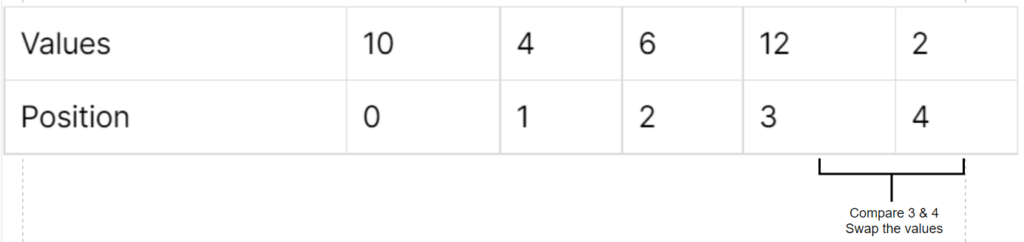
Two pointer algorithm is one of the basic and easy data structures for beginners. It is also commonly asked in most of the interview

In this tutorial, we will learn to apply the two pointer algorithm to find the sum of two numbers in a sorted array

Input

given sorted array
let a = {8 , 12, 24, 30, 44, 54, 60, 61}
sum of two numbers 
let x = 98
Output
44,54

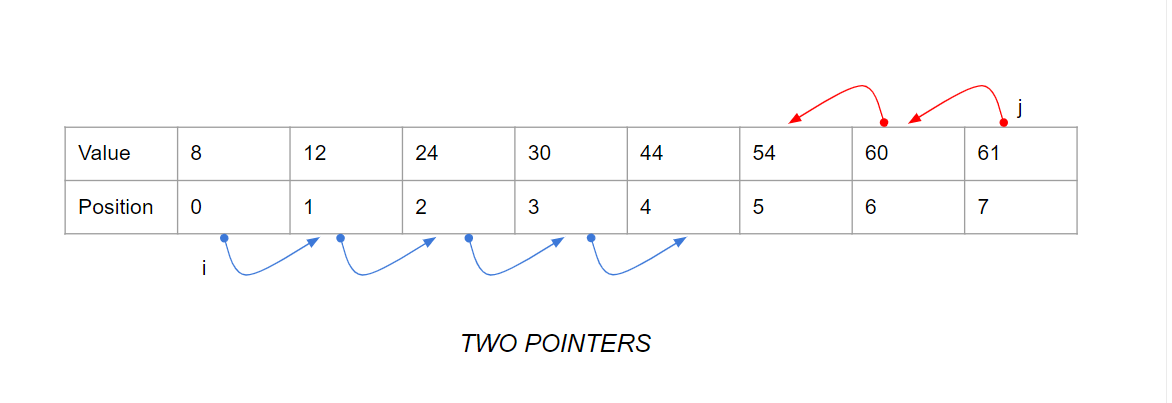
Algorithm explanation

  • The Array should be Sorted in ascending
  • initialize a variable as i with starting position as zero
  • initialize a variable as j with starting position as n-1
  • check the sum of index i & j, if matches then print the value
  • else if the sum is less than the target value then increase the i position
  • else decrease the j position

Example

public class TwoPointersExample {

    private void sumofTwoNumbers(int a[], int x) {
        if (a != null && a.length > 0) {
            int i = 0;
            int j = a.length - 1;
            boolean isFound = false;
            while (i < j) {
                int sum = a[i] + a[j];
                if (x == sum) {
                    System.out.println("The value is " + a[i] + " " + a[j]);
                    isFound = true;
                    break;
                } else if (sum < x) {
                    i++;
                } else {
                    j--;
                }
            }
            if (!isFound) {
                System.out.println("Not able to find with given input");
            }

        } else {
            System.out.println("Not a valid input");
        }

    }

    public static void main(String[] args) {
        int a[] = {8, 12, 24, 30, 44, 54, 60, 61};
        TwoPointersExample example = new TwoPointersExample();
        example.sumofTwoNumbers(a, 98);
        ;
    }
}

Output

The value is 44 54

Related Articles

binary search algorithm
Categories
data structures insertion sort java

insertion sort algorithm

In this article, we will discuss the simple sorting algorithm called insertion sort.

What is insertion sort?

This works in a similar fashion as playing a deck of cards. Assuming two different parts – sorted and unsorted, we need to pick and sort each card from an unsorted part into a sorted part.

Steps to be folowed

The first element in an array is to be considered as already sorted.

The next element is to be taken and compared with the elements in a sorted array.

Insert the element by shifting the elements in the sorted array which are greater than the value to be sorted

Example

import java.util.Arrays;

public class InsertionSort {

	private void sortArray(int[] arr) {

		for (int i = 1; i < arr.length; i++) {
			int key = arr[i];
			int j = i - 1;
			while (j >= 0 && arr[j] > key) {
				arr[j + 1] = arr[j];
				j--;
			}
			arr[j + 1] = key;
		}

	}

	public static void main(String[] args) {
		InsertionSort insertionSort = new InsertionSort();
		int[] arr = { 2, 7, 5, 8, 3, 4, 1, 6 };
		insertionSort.sortArray(arr);
		System.out.println(Arrays.toString(arr));
	}

}

Output

[1, 2, 3, 4, 5, 6, 7, 8]

Related Articles

selection sort
Categories
data structures java selection sort

selection sort

selection sort

In this post, We will learn about the selection sort algorithm in the java language. It is a comparison-based sorting algorithm

Selection sort will select the element from an array, and keep on compare with the remaining elements.

End of each iteration we will obtain the minimum value, After that we will swap the minimum element to the sorted array

Likewise, it will select all the elements in the array and compare them with the remaining element 

Unsorted Input array: [ 12, 4, 6, 7, 2, 5 ]
Sorted Output array:  [ 2, 4, 5, 6, 7, 12 ]

Execution Steps

  1. [2, 4, 6, 7, 12, 5]
  2. [2, 4, 6, 7, 12, 5]
  3. [2, 4, 5, 7, 12, 6]
  4. [2, 4, 5, 6, 12, 7]
  5. [2, 4, 5, 6, 7, 12]

Selection Sort

Time Complexity : O(n^2)

Code

package example;

import java.util.Arrays;

public class SelectionSort {

	private void sortArray(int[] arr) {

		for (int i = 0; i < arr.length; i++) {
			int selectionItem = i;
			for (int j = i + 1; j < arr.length; j++) {
				if (arr[j] < arr[selectionItem]) {
					selectionItem = j;
				}
			}
			int temp = arr[selectionItem];
			arr[selectionItem] = arr[i];
			arr[i] = temp;
		}
	}

	public static void main(String[] args) {
		int[] arr = { 12, 4, 6, 7, 2, 5 };
		SelectionSort selectionSort = new SelectionSort();
		selectionSort.sortArray(arr);
		System.out.println(Arrays.toString(arr));
	}
}

Output

[2, 4, 5, 6, 7, 12]

Related Articles

bubble sort algorithm
Categories
Bubble sort data structures java

bubble sort algorithm

bubble sort algorithm

In this post, we will learn about the bubble sort algorithm. The bubble sort algorithm is one of the important sorting algorithms

It will compare two adjacent elements in an array and swap the right value to the left if it is lesser than left

Bubble Sort

Time Complexity: O(n^2)
Values1012462
Position01234
Input Array
Step 1
Iterate the given array using for loop
Step 2 
Add one more iteration within the for loop again
Step 3
compare the first element with second element
Step 4 
If first element greater than second element swap the two elements
Step 5 
Compare the second element with third element 
Step 6
If Second element is greater than third element, then swap the two elements 
Step 7 
Continue until nth element
Step 1
Step2
Step 3
Step 4
Result of the first iteration

Java Implementation 


public class BubbleSort {

	private void sortArray(int arr[]) {
		for (int i = 0; i < arr.length; i++) {
			boolean isSwap = false;
			for (int j = 0; j < arr.length - i - 1; j++) {
				if (arr[j] > arr[j + 1]) {
					int temp = arr[j + 1];
					arr[j + 1] = arr[j];
					arr[j] = temp;
					isSwap = true;
				}
			}
			if (!isSwap) {
				break;
			}
		}
	}

	public static void main(String[] args) {
		int arr[] = { 10, 12, 4, 6, 2 };
		System.out.println("Array Before sorting");
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + "  ");
		}
		BubbleSort bubbleSort = new BubbleSort();
		bubbleSort.sortArray(arr);

		System.out.println("\nArray After Sorting");
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + "  ");
		}

	}

}

Output

Array Before sorting
10  12  4  6  2  
Array After Sorting
2  4  6  10  12
search in rotated sorted array
Categories
binary search data structures java

search in rotated sorted array

search in rotated sorted array

In this post we will discuss about search in rotated sorted array in efficient way using java

Problem Statement

Input: rotated sorted array
Time Complexity: O(logn)
Efficient Approach: Binary Search

Test Case 1
Input: { 7, 8, 0, 1, 2, 3, 4, 5, 6 }
Target:  8
Output: 1

Test Case 2
Input: { 7, 8, 0, 1, 2, 3, 4, 5, 6 }
Target:  100
Output: -1

Explanation

  • Consider that array doesn’t have duplicates
  • As initial step, we are going to let left pointer =0 & right pointer = array.lenght-1
  • As per binary search we are going to find the mid of the array
  • In case target value matches mid value, then return the mid
  • find the left and right position based on the below solution in iterative way

Solution


public class RotatedBinarySearchExample {

	private int rotatedBinarySearch(int[] nums, int target) {

		// Basic check 
		if (null == nums || nums.length == 0) {
			return -1;
		}
		if (nums.length == 1 && nums[0] == target) {
			return 0;
		}

		int mid = 0;
		int leftPointer = 0;
		int rightPointer = nums.length - 1;

		while (leftPointer <= rightPointer) {

			mid = (leftPointer + rightPointer) / 2;

			if (nums[mid] == target) {
				return mid;
			} else if (nums[leftPointer] <= nums[mid]) { 
				if (target >= nums[leftPointer] && target <= nums[mid]) {
					rightPointer = mid - 1;
				} else {
					leftPointer = mid + 1;
				}

			} else {
				if (target >= nums[mid] && target <= nums[rightPointer]) {
					leftPointer = mid + 1;
				} else {
					rightPointer = mid - 1;
				}
			}
		}
		return -1;
	}

	public static void main(String[] args) {
		RotatedBinarySearchExample rotatedBinarySearchExample = new RotatedBinarySearchExample();
		int[] array = { 7, 8, 0, 1, 2, 3, 4, 5, 6 };
		int targetNumber = 8;
		int output = rotatedBinarySearchExample.rotatedBinarySearch(array, targetNumber);
		System.out.println(output);
	}

}

Output

1

Reference

binary search algorithm
Categories
binary search data structures java

binary search algorithm

Binary search algorithm is one of the fastest way to identify the element from an sorted array. It is also the commonly asked data structure interview questions.

It works based on divide and conquer mechanism. It will divide the given array into 2 parts and discard the one part. So it will works faster for a big array compared to linear search.

Time complexity of Binary Search is O(logn)

Below is the give array structure

With the above given array we have to find the position of 9, Using linear search we can find easily, But the time complexity will be O(N)

Below is java code snippet to find the position using Binary Search 

public class BinarySearchExample {

	private int binarySearch(int[] array, int target) {
		int leftIndex = 0;
		int rightIndex = array.length - 1;
		while (leftIndex <= rightIndex) {
			// find the middle Index
			int middleIndex = (leftIndex + rightIndex) / 2;
			if (array[middleIndex] == target) {
				return middleIndex;
			}
			if (target > array[middleIndex]) {
				// ignoring the left side of array
				leftIndex = middleIndex + 1;
			} else {
				// ignoring the right side of array
				rightIndex = middleIndex - 1;
			}
		}
		return -1;
	}

	public static void main(String[] args) {
		int[] i = { 2, 3, 5, 6, 7, 9,10 };
		int targetNumber = 9;
		BinarySearchExample object = new BinarySearchExample();
		int output = object.binarySearch(i, targetNumber);
		System.out.println(output);
	}

}
Output
5